Векторна графіка в LaTeX заcобами TikZ

Олександр Рудик

Векторна графіка в LaTeX заcобами TikZ

(Комп'ютер у школі та сім'ї — 2012. — № 7. — С. 43–46, № 8. — С. 35–38)

Передмова

      Ця публікація є безпосереднім продовженням попередньої публікації автора, що описувала можливості LaTeX 90-x років XX століття. Того, що давало можливість зручно для автора підготувати текст з численними математичними формулами зі складною структурою. Підготувати у формі, максимально доступній для сприйняття читачем. При цьому можна було, наприклад, точно подати графіки функцій і легко подати зображення розгорток многогранників. Для простих ілюстрацій планіметричних та стереометричних задач цього було достатньо. Але потреба подавати складні схеми, діаграми та ще й у кольорі потребувала нововведень. Таким нововведенням, що долучило до LaTeX графічний векторний редактор, став пакет Pgf/TikZ (входить до складу MiKTeX). Ця публікація є спробою подати стислий опис можливостей пакету Pgf/TikZ без «занурення до дна» детального опису — 725 сторінок формату А4 англійською мовою. Наш стислий опис неповний, але достатній для успішної роботи у більшості випадків. Посилання на ресурси глобальної мережі дозволить читачам, образно кажучи, «не лише пірнути до дна, але й покопатися». В кінці публікації описано процес розширення вільнопоширюваного редактора векторної графіки Inkscape до експорту результатів у TikZ.
      Публікацію призначено для учнів класів з поглибленим вивченням математики чи фізики, студентів математичних і фізичних спеціальностей, вчителів математики й фізики, наукових працівників.

      1. Спосіб використання

      Трансляція — перетворення формату з tex на pdf — результат виконання такої вказівки: pdflatex назва файлу.tex. Тут і далі курсивом виділено назви понять, замість яких користувач має записати назви об'єктів або числові величини.
      У преамбулі потрібно замовити:

використання пакету вказівкою: \usepackage{tikz};
використання біліотек пакету. Наприклад, таким чином:

\usetikzlibrary{positioning,arrows,through,patterns,calc}

Параметри вказують на можливість такого:
- positioning — відносного позиціонування;
- arrows — креслення стрілок;
- through — проведення кола через задану точку;
- patterns — штрихування;
- calc — обчислень.;

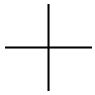
Всередині середовища document вказівки рисунку розташовують у середовищі tikzpicture або використовують як аргумент вказівки \tikz. Наприклад, і код:

\tikz{\draw (-1,0) -- (1,0);
      \draw (0,-1) -- (0,1);}

і код:\begin{tikzpicture}\draw (-1,0) -- (1,0); \draw (0,-1) -- (0,1); \end{tikzpicture}

призведуть до одного й того самого зображення двох взаємно перпендикулярних відрізків.

      При цьому кожну вказівку завершують крапкою з комою. У поданому прикладі використано вказівку \draw. Згідно із замовчуванням TikZ тлумачить усі розміри у сантиметрах, але їх можна задати й стандартним способом. Розташування центра координат (0,0) є відносним.
      Середовище tikzpicture має параметр scale, за домомогою якого можна збільшувати чи зменшувати розмір рисунку без зміни величин координат об'єктiв на рисунку.

2. Синтаксис вказівок

      Загальний синтасис вказівок такий:
\command [parameters] (name) {contents} arguments;

Тут
command — вказівка;
parameters — перелік параметрів через кому;
name — назва створюваного об'єкта (на уподобання користувача);
contents — вміст об'єкта (може містити інші об'єкти);
arguments — аргументи, наприклад, координати точок шляху, розміри чи інші вказівки без \.
      Обов'язковою є наявність лише власне вказівки. В tikz багато вказівок, але у багатьох випадках достатньо використання лише path i node.
      Вказівка \path створює контур. Її параметри описують, як цей контур використовують:
draw — лише накреслити контур;
fill — лише заповнити;
fill,draw — накреслити контур і заповнити;
use as bounding box — використати контур як обмеження зображення.
Замість \path[draw], \path[fill], \path[shade,draw], … використовують скорочення \draw, \fill, \shadedraw.
      Як параметр \path також вказують на наявність і напрям стрілок, колір, товщину лінії тощо.
      Колір можна задати таким чином:

назвою кольору, попередньо означеною в LaTeX і пакеті xcolor. Наступні назви є завжди досяжними: black, blue, brown, cyan, darkgray, gray, green, lightgray, lime, magenta, olive, orange, pink, purple, red, teal, violet, white, yellow;
змішуванням кольорів з попередньо означеними назвами. Синтаксис запису змішування такий: колір1!відсоток!колір2. У результаті отримують колір, що містить відсоток% кольору1 і (100 – відсоток)% кольору2. Наприклад, red!20!yellow означає змішування червоного й жовтого кольорів у пропорції 20:80. Білий колір можна не вказувати. Дії змішування виконують у порядку їх запису зліва направо — див. далі приклад задання стилю вузла для вказівки \node.

Запровадження нових кольорів здійснюють вказівками:

\definecolor{своя назва}{rgb}{інтенсивність червоного, інтенсивність зеленого, інтенсивність блакитного}, де інтенсивності кольорів задано дійсними числами в межах від 0 до 1 включно;
\colorlet{своя назва}{код кольору, заданий допустимим чином}.

      Зміна кольору тексту — результат дії вказівки: \textcolor{колір}{text}.
      Щодо решти параметрів — див. далі опис вказівки \draw та інших оболонок над \path.
      Аргументами є координати точок, що через які має проходити контур. В tikz можна використати такі способи задання координат (після назви подано приклад використання):

декартові відносні (1,5);
декартові абсолютні на аркуші (11pt, 22mm);
полярні кут-відстань (3:2);
декартові відносно попередньої точки ++(0,1);
декартові відносно початкової точки +(-1,2);
барицентричні відносно двох точок (1,2)!.3!(3,4) — координати точки, розташованої на відстані 3/10 шляху з (1,2) до (3,4);
відстань на промені (1,2)!3cm!(3,4) — координати точки, розташованої на відстані 3 см від від початку променя (1,2) на промені, що містить точку (3,4);
проекція на дану пряму (1,2)!(3,0)!(3,4) — координати проекції точки (3,0) на пряму, що містить точки (1, 2) і (3, 4).

      Координати точок, між якими потрібно провести лінію, розділяють символами --.
      Назви об'єктів (у круглих дужках), межі яких потрібно сполучити, розділяють символами edge:
\path (об'єкт₁) edge (об'єкт₂);
      Вказівка \node створює вузол, що зазвичай містить текст. Її параметрами можуть бути стиль тексту, колір, інформація щодо наявності, форми й кольору меж, розташування відносно інших об'єктів тощо. Розташовують вузол у точці з координатами (x, y) за допомогою аргумента at (x, y). Розташування відносно інших об'єктів здійснюють, використовуючи библиотеку positioning. Наприклад, вказівка:
\node[right of=назва₁] (назва₂) {текст}
створить вузол назва₂ праворуч від вузла назва₁ і розташує в ньому текст.
      Cтиль оформлення вузла задають, якщо кілька вузлів потрібно зобразити однаковим чином. Для цього використовують вказівку \tikzstyle. Подамо приклад такого використання з коментарями після символа %.

\tikzstyle{format} = [ rounded rectangle, thick, minimum size=1cm, draw=red!50!black!50, top color=white, bottom color=red!50!black!20, font=\itshape] % прямокутник зі зглаженими краями
% контур жирною лінією
% мінімальний розмір
% контур має колір: 25% червоного + 25% чорного + 50 білого
% білий згори для градієнтної заливки згори донизу
% 10% червоного + 10% чорного + 80% білого знизу
% похилий шрифр тексту

Після такого означення стиль format можна вказати як параметр відповідного вузла \node. Зображення

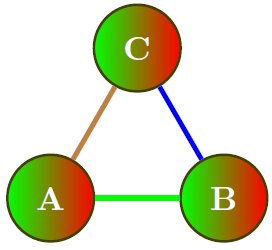
створено за допомогою такого коду (тут і далі подано лише вміст середовища tikzpicture):

\tikzstyle{format} = [
 circle,
 thick,
 minimum size=1cm,
 draw=green!50!red!50!black,
 right color=red,
 left color=green,
 font=\bfseries 
]
\node[format] (A) at (0,0)     {\textcolor{white}{A}};
\node[format] (B) at (2,0)     {\textcolor{white}{B}};
\node[format] (C) at (1,1.732) {\textcolor{white}{C}};
\path[green, ultra thick] (A) edge (B);
\path[blue,  ultra thick] (B) edge (C);
\path[brown, ultra thick] (C) edge (A);

3. Лінії

Для зображення ліній використовують вказівку \draw. Довільну накреслену криву можна замкнути таким чином:
\draw … -- cycle;
У квадратних дужках після \draw через кому можна вказати:

товщину (подано у порядку зростання):ultra thin very thin thin semithick thick very thick ultra thick або вказати товщину явно, наприклад: line width=4pt ;
тип:solid dotted densely dotted loosely dotted dashed densely dashed loosely dashed dashdotted densely dashdotted loosely dashdotted dashdotdotted densely dashdotdotted loosely dashdotdotted Подамо зображення згаданих типів у тому самому порядку переліку.
стрілку:
- стрілка, спрямована на початкову або на кінцеву точку: <- або ->
- стрілки на обох кінцях лінії: <–>
- подвійна стрілка ліворуч або праворуч: <<- або ->>
- подвійні стрілки на обох кінцях лінії: <<->>
Подамо зображення, отримане за допомогою такого коду:\draw[->] (0,0) -- (2,0); \draw[>->>] (0,-.5) -- (2,-.5); \draw[|<->|] (0,-1) -- (2,-1); \draw[o-*] (0,-1.5) -- (2,-1.5); \draw[)-)] (0,-2) -- (2,-2);
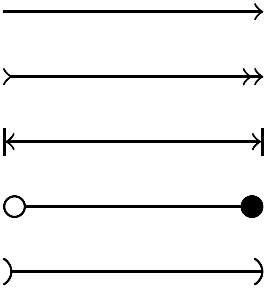
колір (див. вище пункт 2. Синтаксис вказівок).

      Задані величини параметрів застосовують до всіх фігур, що виводять вказівкою \draw до наступного переозначення параметрів у квадратних дужках.
      Після вказівки \draw (з визначенням величин параметрів у квадратних дужках чи без цього) у круглих дужках потрібно вказати початкову точку кривої, центр фігури (для кола, еліпса или дуги) или одну из точок прямокутної області. Наприклад, \draw(2,3) .
      Далі записують модифікатор — тип лінії. Тлумачення чисел у круглих дужках після модифікатора залежить від модифікатора. Різні модификатори можна розташувати послідовно всередині однієї вказівки \draw.
      Проведення відрізка до точки (x, y) задають так: -- (x, y). Ламану з кількох ланок можно накреслити, вказавши координати послідовних вершин у дужках через кому. Наприклад, вказівка:\draw (0,0) -- (1,1) -- (0,1) -- (1,0) -- (0,0); зобразить ламану, утворену діагоналями квадрати й парою його протилежних сторін, паралельних осі абсцис Ox.

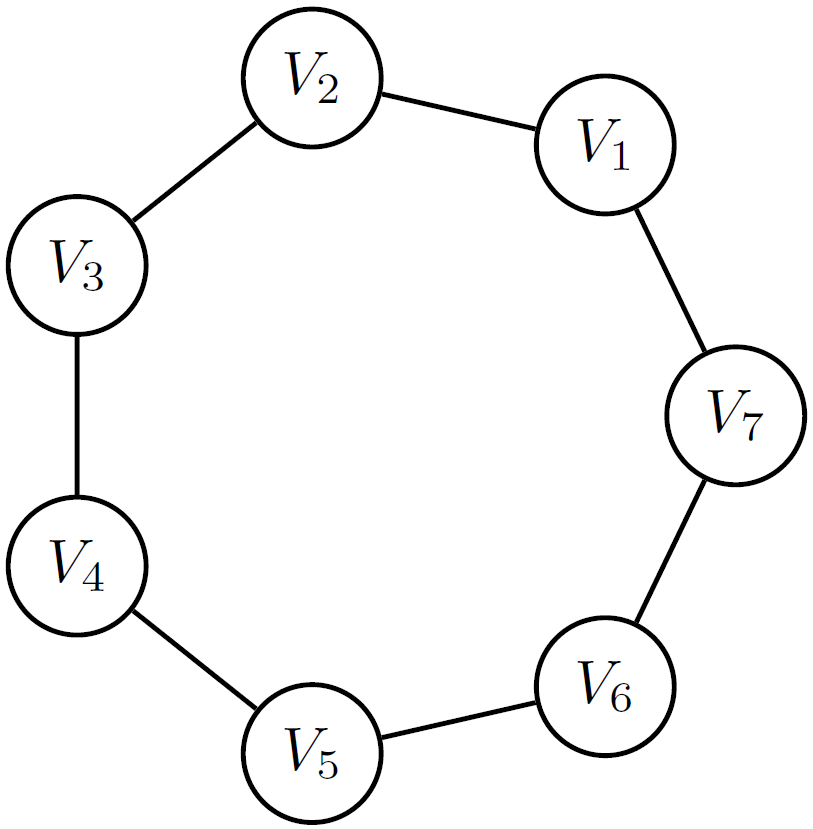
Породження вузлів до проведення ламаної подамо прикладом такого коду:

\tikzstyle{every node}=[draw,shape=circle,thick];
\node (v1) at   (360/7:2) {$V_1$};
\node (v2) at (2*360/7:2) {$V_2$};
\node (v3) at (3*360/7:2) {$V_3$};
\node (v4) at (4*360/7:2) {$V_4$};
\node (v5) at (5*360/7:2) {$V_5$};
\node (v6) at (6*360/7:2) {$V_6$};
\node (v7) at      ( 0:2) {$V_7$};
\draw[thick] (v1) -- (v2) -- (v3)-- (v4) -- (v5) -- (v6) -- (v7) -- (v1);

що породжує таке зображення:

Породження вузлів при проведенні ламаної подамо прикладом такого коду:

\draw (0,0) node [below left]  {$A_1$} -- 
      (1,0) node [below right] {$A_2$} -- 
      (1,1) node [above right] {$A_3$} -- 
      (0,1) node [above left]  {$A_4$} -- 
cycle;

що породжує таке зображення:

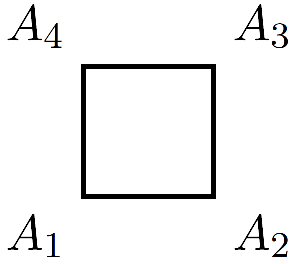
      Ґратку записують, наприклад, так: \draw[step=.1cm] (1,2) grid (3,4);. У поданому прикладі параметр step визначає крок ґратки, а пари чисел до й після модификатора grid – область [1,2]×[3;4] для покриття ґраткою.
      Круг з радіусом r записують так: circle (r).
      Еліпс з осями a й b записують так: ellipse (a and b).
      Дугу круга з кутовим аргументом від α до θ й радіусом r записують так: arc (α : θ : r).
      Дугу еліпса з кутовим аргументом від α до θ й осями a й b записують так: arc (α : θ : a and b). При зображенні дуг центр кола чи еліпса розраховується автоматично, а координати arc задають початкову точку дуги.
      Прямокутник, у якому координати однієї вершини задано безпосередньо після запису вказівки \draw до модифікатора, а протилежна вершина має координати (x, y), записують так: rectangle (x, y). Заокруглити кути прямокутника дугою кола з радіусом r можна, вказавши параметр [rounded corners=r].
      Кубічну криву Без'є задають такою вказівкою (A) .. controls (X) and (Y) .. (B). Тут (A) та (B) — кінці кривої, (X) та (Y) — опорні точки, розташування яких впливає на форму кривої. Відсутність частини and (Y) означає (Y) = (X). При цьому можна створювати вузли у точках параметризованої кривої (параметр зростає від 0 до 1 при русі точки від початку до кінця), задаючи величину параметра — див. результат виконання такого коду:

\draw[line width=2pt] (0,0) .. controls (1,3) .. (4, 0)
node[pos=0,left] {0}
node[pos=.2,left] {0.2}
node[pos=0.7,above]{0.7}
node[pos=1,right]{1}

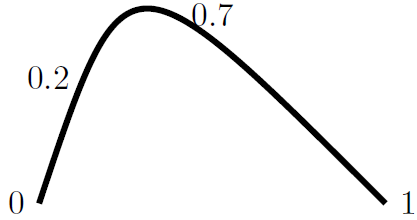
Кубічну криву можна задати, вказавши початкову й кінцеву точки та кутові аргументи дотичних векторів у цих точках. Наприклад, таким чином:

\draw[line width=2pt,->>] (0,0) to [out=150, in=180] (4,2);
\draw[line width=2pt,->]  (0,0) to [out=-90, in=0]   (4,2);

4. Заповнення

      Замкнений контур з заповненням того самого кольору можна намалювати з допомогою вказівки \fill, синтаксис використання якої такий самий, як для вже розглянутої вказівки \draw.
      При різних кольорах контуру й заповнення використовують таку вказівку:
\filldraw[fill=колір заповнення, draw=колір контуру] запис контуру такий самий, як для \draw
      Прозорість визначають параметром opacity, що набуває дійсних величин у межах від 0 до 1. Повній непрозорості відповідає 1.
      Різні прозорості тла й контуру задають відповідно параметрами fill opacity й draw opacity.
      Для прикладу подамо зображення

створене за допомогою такого коду:\draw[step=1,gray] (-4,-3) grid (4,3); \draw[thick,violet,densely dashed] (0,0) ellipse (4 and 3); \draw[thick,red,densely dotted] (0,0) circle (3); \fill[thick,green] (0,1.5) arc (90:0:2 and 1.5) arc (180:-90:.5) -- cycle; \fill[thick,cyan,opacity=0.5] (-1.5,1.5) rectangle (-2.5,-1.5); \draw[thick,blue] (0,0) .. controls (1,-1) and (-1,-1) .. (0,-3);

5. Перетворення зображення

      Поворот фігури здійснюють, вказавши у градусах параметр rotate вказівки виводу зображення — \draw, \fill або \filldraw)
      Паралельне перенесення на вектор v(x, y) можна здійснити, вказавши параметри: xshift=x, уshift=у. Якщо перенесення здійснюють у вертикальному чи горизонтальному напрямку, то відповідне надання нульової величини *shift=0 можна не записувати.
      Вирізання частини зображения, обмеженої контуром, без зображення цього контуру здійснюють вказівкою \clip, синтаксис використання якої щодо запису контуру такий самий, як для розглянутої вказівки \draw. Ця вказівка нічого не малює, але впливає на зображення фігур, заданих наступними за нею вказівками.
      Вирізання частини зображения, обмеженої контуром, разом із зображенням цього контуру здійснюють вказівкою \draw з опцією clip (вказаною у квадратних дужках).
      Обмеження дії вирізання зображення здійснюють розташуванням вказівки вирізання й наступних вказівок побудови фрагментів зображення всередині середовища \begin{scope}...\end{scope}.
      Для прикладу подамо зображення

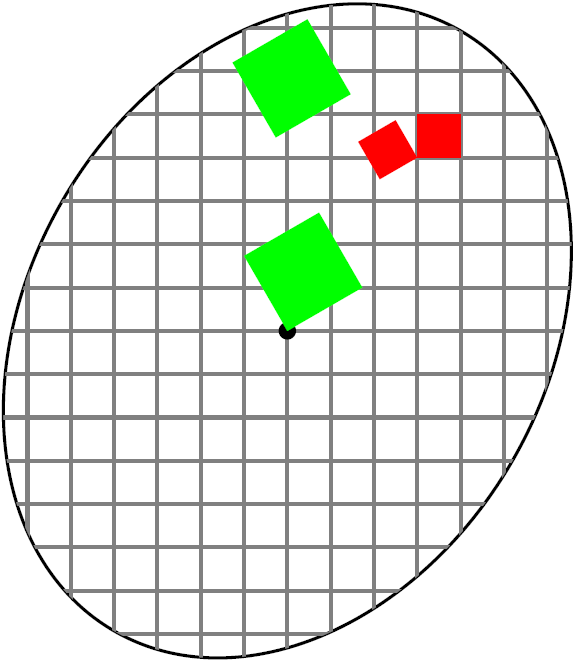
створене за допомогою такого коду:\draw[rotate=60,clip] (0,0) ellipse (4 and 3); \draw[step=.5,gray] (-4,-4) grid (4,4); \fill[black] (0,0) circle (.1); \fill[thick,green,rotate=30] (0,0) rectangle (1,1); \fill[thick,green,rotate=30,xshift=1cm,yshift=2cm] (0,0) rectangle (1,1); \fill[thick,red,xshift=1.5cm,yshift=2cm] (0,0) rectangle (.5,.5); \fill[thick,red,xshift=1.5cm,yshift=2cm,rotate=120] (0,0) rectangle (.5,.5);

      Поданий приклад наочно переконує, що результат повороту й паралельного перенесення залежить від порядку виконання дій.

      6. Штрихування

      Для створення досконалих креслень можна скористатися бібліотекою patterns. Назви штрихувань такі:

horizontal lines;
vertical lines;
north east lines;
north west lines;
grid;
crosshatch;
dots;
crosshatch dots;
fivepointed stars;
sixpointed stars;
bricks;
checkerboard.

Усі ці штрихування подамо зображенням у порядку: зліва направо у першому рядку, а потім — зліва направо у другому рядку

У поданому зображенні [scale=2], а штрихування горизонтальними лініями отримано таким чином:

\draw[pattern=horizontal lines] (0,0) rectangle (2,2);

Поєднання заливки кольором і штрихування подамо зображенням фрагменту цегляної стіни

Це зображення створено таким кодом:\fill[red] (0,0) rectangle (1,1); \fill[pattern=bricks,pattern color=white] (0,0) rectangle (1,1);

при [scale=2].

7. Тінь

      Подамо ефекти тіні з відповідними кодамим.
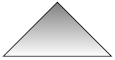\path[shade,draw] (1,0) -- (2,1)--(3,0)--cycle;

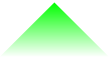\shade[top color=green] (1,-2)--(2,-1)--(3,-2)--cycle;

\shade[left color=red, right color=yellow] (1,-3) rectangle (3,-4);

\shade[draw,shading=radial, inner color=green](1,-6) rectangle (3,-5);

\shade[shading=rectangle, ball color=blue] (1,-8) rectangle (3,-7);

\shade[shading=ball, ball color=red] (1,-9) circle (.4);
\shade[shading=ball, ball color=yellow] (2,-9) circle (.4);
\shade[shading=ball, ball color=green] (3,-9) circle (.4);

8. Координати й обчислення

      Означення точки за її координатами (x, y) здійснюють такою вказівкою:
\coordinate (назва точкиy) at (x, y);
      Означення підпису та його розташування визначають аналогічно. Наприклад, таким чином:
\coordinate [label=left:$A\Rightarrow B$] (pointName) at (0,1);      Розташування тексту відносно точки можна вказати індентификаторами left, right, below або above. Якщо замість них вказати число, його буде розтлумачено як градусну міру кута повороту підпису від осі абсцис. Визначену таким чином точку можна використати замість прямого вказування координат. Наприклад, код:

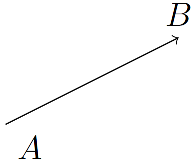
\coordinate [label=-45:$A$] (A) at (0,0);
\coordinate [label=above:$B$] (B) at (2,1);
\draw [->] (A) -- (B);

породжує таке зображення:

Якщо у підпису потрібно використати кому, яку зазвичай тлумачать як роздільник координат, то потрібно скористатися вказівкою \noexpand{...}.
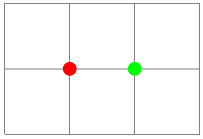
З допомогою бібліотеки \usetikzlibrary{calc} можна здійснювати лінійні операції з координатами точок, які записують між знаками долара. Наприклад, таким чином:

\draw[gray] (0,0) grid (3,2);
\fill [red]   ($(.3,.2)+(.7,.8)$) circle (3pt);
\fill [green] ($5*(.4,.2)$) circle (3pt);

для отримання такого зображення.

Зображення

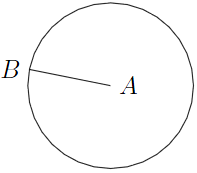
створене за допомогою такого коду:

\coordinate [label=right:$A$] (A) at (0,0);
\coordinate [label=left :$B$] (B) at (-1.25,0.25);
\draw (A) -- (B);
\draw (A) let \p1 = ($ (A) - (B) $) in circle ({veclen(\x1,\y1)});

В останній вказівці:

запроваджено векторну змінну \p1, координати якої — \x1 i \y1 — є різницями відповідних координат точок A i B. Тут число 1 — номер набору взаємозв'язаних змінних;
радіус кола визначено як довжину вектора — veclen — з цими координатами.

9. Перетин відрізків і кіл

Точка перетину двох прямих — те що можна знайти й зобразити. Потрібно лише попередньо задати лінії. Наприклад, такий код:

\draw[gray] (0,0) grid (3,2);
\draw (0,0) coordinate (A) -- (3,1) coordinate (B)
      (0,2) coordinate (C) -- (2,0) coordinate (D);
\fill[red] (intersection of A--B and C--D) circle (2pt);

породить таке зображення:

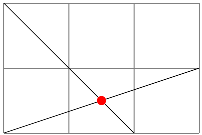
Таким чином знаходять перетин саме прямих, а не відрізків. Щоб у цьому пересвідчитися, достатньо отримати таке зображення

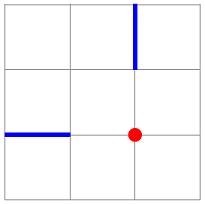
за допомогою такого коду:

\draw[gray] (0,0) grid (3,3);
\draw[ultra thick,blue] (0,1) coordinate (A) -- (1,1) coordinate (B)
                        (2,2) coordinate (C) -- (2,3) coordinate (D);
\fill[red] (intersection of A--B and C--D) circle (3pt);

Точки перетину двох кіл — наступні об'єкти для знаходження. Потрібно не задати лінії, але й вказати номер точки перетину. Наприклад, такий код :

\coordinate [label=left:$A$]  (A) at (0,0);
\coordinate [label=right:$B$] (B) at (3,4);
\coordinate                   (X) at ($(A)+(3,0)$);
\node (E) [draw,circle through=(X),label=left:$E$] at (A) {};
\node (F) [draw,circle through=(A),label=right:$F$] at (B) {};
\coordinate[label=-60:$C$] (C) at (intersection 1 of E and F);
\coordinate[label=left:$D$] (D) at (intersection 2 of E and F);
\fill (A) circle (2pt);
\fill (B) circle (2pt);
\fill[red]   (C) circle (3pt);
\fill[green] (D) circle (3pt);

породить таке зображення:

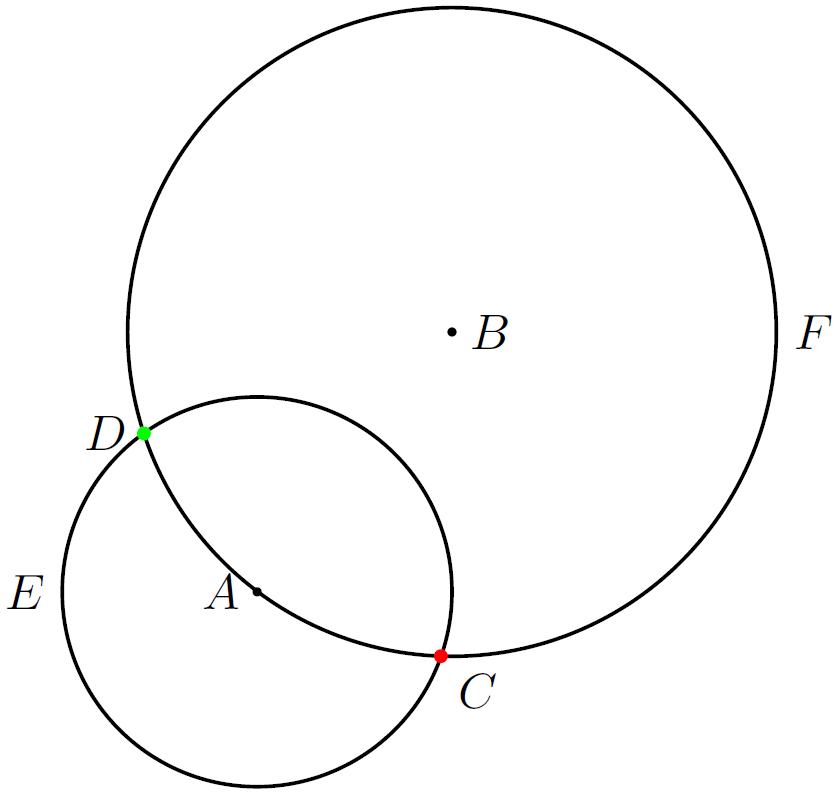
Це зображення отримано при [scale=0.5] — параметрі середовища tikzpicture.
Знаходження точки дотику двох кіл може закінчитися невдачею. Розглянемо код:

\coordinate [label=left:$A$]  (A) at (0,0);
\coordinate [label=right:$B$] (B) at (4,3);
\coordinate (X) at ($(A)+(2,0)$);
\coordinate (Y) at ($(B)+(3,0)$);
\node (E) [thick,draw,circle through=(X),label=left:$E$]  at (A) {};
\node (F) [thick,draw,circle through=(Y),label=right:$F$] at (B) {};
\coordinate[label=right:$C$] (C) at (intersection 1 of E and F);
\coordinate[label=left:$D$]  (D) at (intersection 2 of E and F);
\fill (A) circle (2pt);
\fill (B) circle (2pt);
\fill[red]   (C) circle (3pt);
\fill[green] (D) circle (3pt);

Виконання цього коду породжує таке зображення:

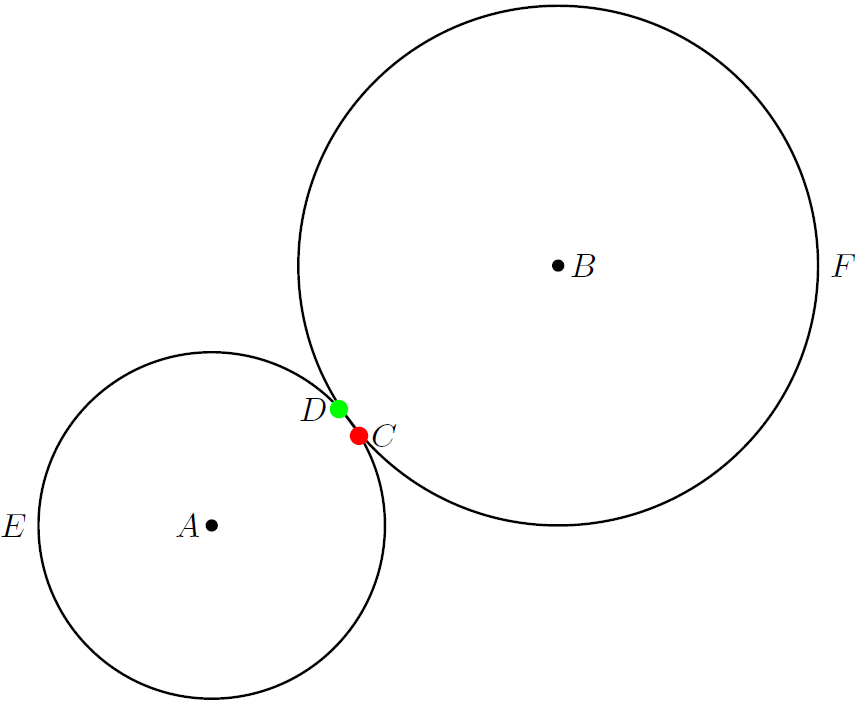
незважаючи на те, що координати точки дотику кіл - скінчені десяткові дроби. Схоже зображення з двома точками перетину отримаємо при заміні координат точки B на (0,5) чи (5,0), коли координати точки дотику цілі.
Порожня множина перетину двох кіл, наприклад, якщо у коді змінити координати точки B на (4,4), призводить до повідомлення про неможливість визначити корінь квадратний від'ємного числа.
Точки перетину кола й прямої можна знайти, наприклад, за допомогою такого коду:

\coordinate [label=left:$O$]  (O) at (0,0);
\coordinate (X) at ($(O)+(5,0)$);
\node (E) [draw,thick,circle through=(X),label=left:$E$]  at (O) {};
\coordinate (A) at (3, 5) {};
\coordinate (B) at (5,-5) {};
\draw[thick] (A) -- (B);
\coordinate[label=right:$C$] (C) at (intersection 1 of E and A--B);
\coordinate[label=right:$D$] (D) at (intersection 0 of E and B--A);
\fill        (O) circle (2pt);
\fill[red]   (C) circle (4pt);
\fill[green] (D) circle (4pt);

Виконання цього коду породжує таке зображення:

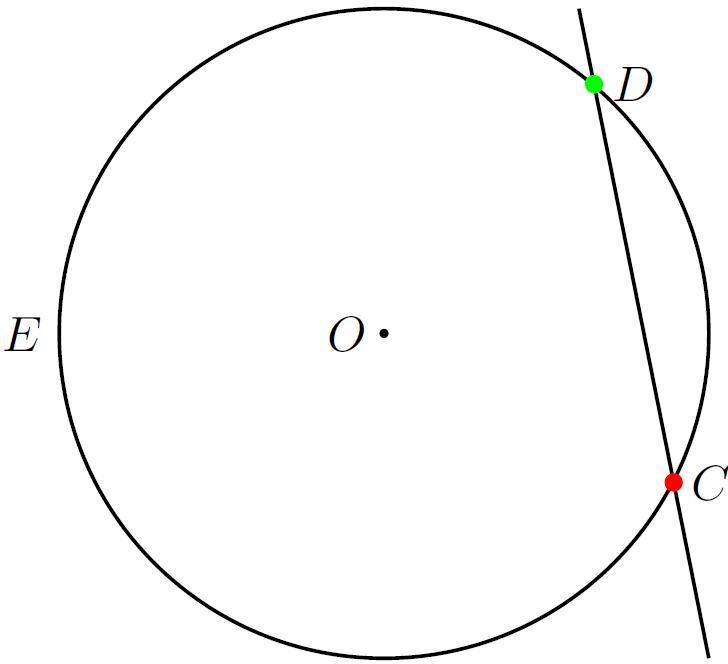
Знаходження точки дотику кола й прямої може закінчитися невдачею. Розглянемо код:

\coordinate [label=left:$O$]  (O) at (0,0);
\coordinate (X) at ($(O)+(5,0)$);
\node (E) [draw,thick,circle through=(X),label=left:$E$]  at (O) {};
\coordinate (A) at ($(25/4,0)$) {};
\coordinate (B) at ($(0,25/3)$) {};
\draw[thick] (A) -- (B);
\coordinate[label=60:$C$] (C) at (intersection 1 of E and A--B);
\coordinate[label=-120:$D$] (D) at (intersection 0 of E and B--A);
\fill        (O) circle (2pt);
\fill[red]   (C) circle (3pt);
\fill[green] (D) circle (3pt);

Виконання цього коду породжує таке зображення:

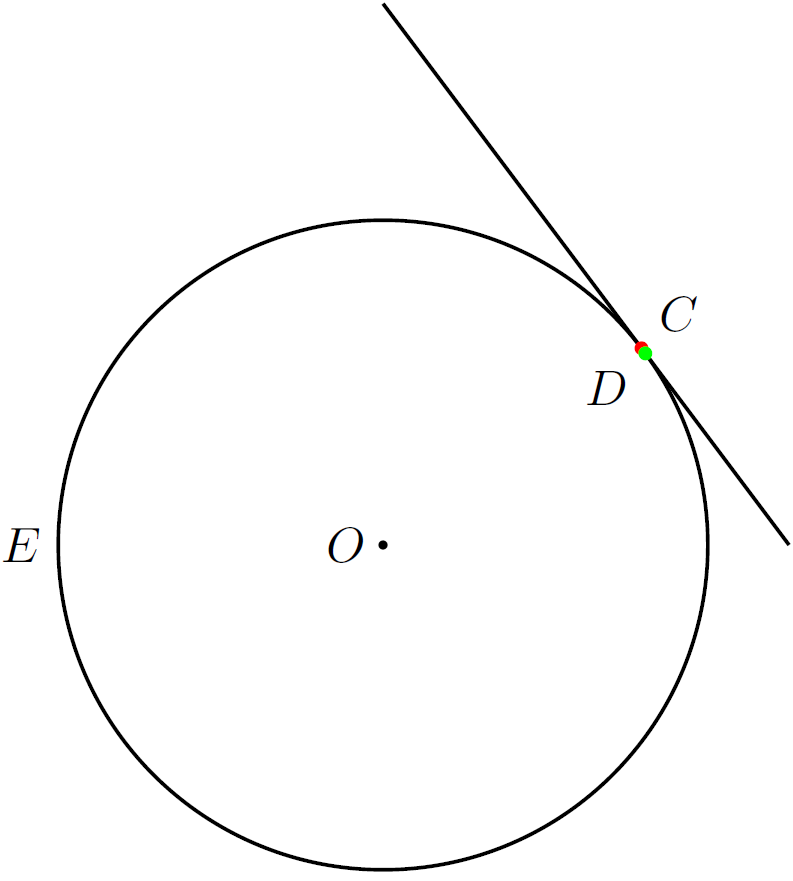
Те, що отримано дві різні точки перетину можна пояснити виконанням наближених обчислень. Гірше те, що зображення цих точок можна розрізнити.
Змінимо код таким чином: координати точок A та B (кінці зображуваного відрізка) змінимо відповідно на (5,5) та (5,–5). Це випадок вертикальної прямої AB, розташованої праворуч від центра кола О на відстані 5 (радіус кола). У цьому випадку зображення точок C й D ми не зможемо розрізнити.

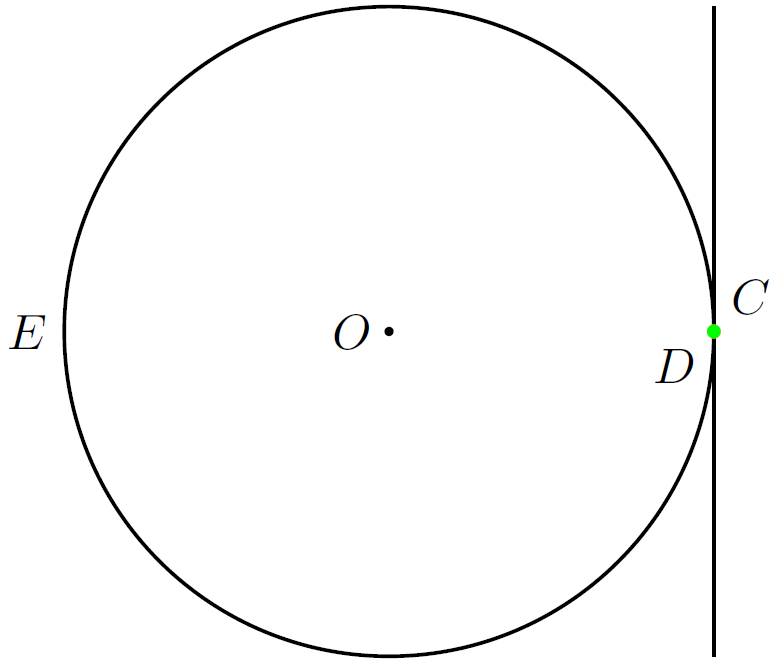
Якщо пряма не має точки перетину (наприклад, коли координати точок A та B змінити на (6,5) та (6,–5) ), точки C й D буде розташовано в околі основи перпендикуляра, опущеного О на пряму AB. Для вертикальної прямої ці зображення зіллються, але для похилої їх можна розрізнити.

10. Цикли

Можливість роботи з циклами проілюструємо трьома прикладами, подаючи спочатку код, а потім породжене ним зображення.

\draw[->] (-3.5,0) -- (4,0) node [below] {$x$}; \foreach \x in {-3,...,3} \draw (\x,0) -- (\x,-0.1) node [below] {$\x$};

Зауважимо таке: змінну \x лічильник циклу розташовано між символами S для коректного виведення від'ємних чисел (знак –, а не дефіс -).

\foreach \x in {0,25,...,100} \shade[ball color=yellow!\x !red] ($0.04*(\x ,0)$) circle (4mm);

\foreach \x in {10,8,...,2} \draw[fill=green!\x0] (-0.1*\x - 1, -0.1*\x ) rectangle (0.1*\x + 1, 0.1*\x );

11. Розширення Inkscape до експорту результатів у TikZ

Оточення picture, описане у попередній публікації, мало свій засіб візуального програмування — TeXCad. Цей засіб важко назвати графічним редактором завдяки істотним відмінностям між кінцевим зображенням та тим, що бачить користувач у процесі створення зображення. Візуальне програмування для TikZ можна здіснити, використавши вільнопоширюваний редактор векторної графіки Іnkscape. За адресою http://code.google.com/p/inkscape2tikz/ — подано опис розширення Inkscape до експорту результатів у код TikZ. Таке розширення отримують, cкопіювавши у теку розширень такі файли:

на які є посилання у вказаному джерелі.
      Для Windows такою текою розширень є inkscape/share/extensions.
      Для Linux та OSX такою текою розширень є home/.inkscape/extensions. При використанні Inkscape 0.47 такою текою є home/.config/inkscape/extensions. Для Linux та OSX потрібно також скопіювати у ту саму теку файли: inkex.py, simplestyle.py, simplepath.py. Їх мають поширювати разом з Inkscape. Їх також можна завантажити з адреси http://inkscape2tikz.googlecode.com/hg/svg2tikz/inkexlib/
      Для експорту даних після завершення роботи над зображенням у середовищі потрібно натиснути кнопку меню Додатки, а у випадному меню вибрати Export і Export to Tikzpath …

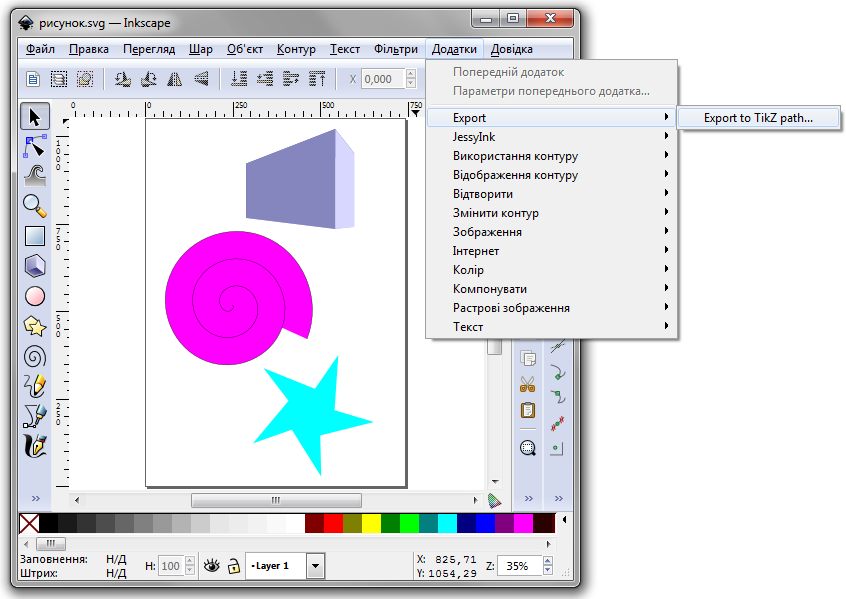
Далі у вікні Export to Tikz path:

вибрати виведення Tikzpicture;
вказати назву файлу, у який буде здійснено виведення. Наприклад, Tikzpicture.tex. Цей файл буде розташовано у вже згаданій теці розширень. Природньо, для успішного здійснення експорту потрібно передбачити право на запис у цю теку;
натиснути кнопку Застосувати.

У новому вікні з'явиться повідомлення про перебіг експорту. Для завершення потрібно натиснути кнопку Гаразд.

Для поданого зображення експортований код має такий вигляд (з точністю до пропусків та ознак кінця рядка):

\definecolor{cff00ff}{RGB}{255,0,255} \definecolor{c00ffff}{RGB}{0,255,255} \definecolor{cafafde}{RGB}{175,175,222} \definecolor{c353564}{RGB}{53,53,100} \definecolor{ce9e9ff}{RGB}{233,233,255} \definecolor{c4d4d9f}{RGB}{77,77,159} \definecolor{cd7d7ff}{RGB}{215,215,255} \definecolor{c8686bf}{RGB}{134,134,191} \begin{tikzpicture}[y=0.80pt, x=0.8pt,yscale=-1, inner sep=0pt, outer sep=0pt] \path[draw=black,fill=cff00ff,line join=miter,line cap=butt,line width=0.800pt] (248.5714,535.2193) .. controls (259.3154,540.0899) and (247.3066,552.1049) .. (240.4762,553.0764) .. controls (221.9660,555.7092) and (210.9890,534.8605) .. (212.8571,519.0288) .. controls (216.1987,490.7095) and (246.9887,475.9577) .. (272.8572,481.6479) .. controls (310.8202,489.9985) and (329.8036,531.8707) .. (320.0000,567.6003) .. controls (306.9334,615.2222) and (253.6288,638.5393) .. (208.0952,624.5050) .. controls (150.7958,606.8442) and (123.1041,541.9595) .. (141.4286,486.6478) .. controls (163.6220,419.6580) and (240.1627,387.5705) .. (305.2382,410.2193) .. controls (381.9273,436.9101) and (418.4230,525.1510) .. (391.4286,599.9813) .. controls (360.2624,686.3758) and (260.2934,727.2880) .. (175.7142,695.9336) .. controls (79.6100,660.3067) and (34.2757,548.5907) .. (70.0000,454.2668) .. controls (110.0774,348.4497) and (233.5536,298.6892) .. (337.6191,338.7908) .. controls (453.1516,383.3111) and (507.3413,518.5574) .. (462.8571,632.3622); \path[fill=c00ffff] (654.2857,869.5051) -- (500.6957,907.9328) -- (503.4788,1025.6444) -- (419.4699,891.4465) -- (308.3795,930.4682) -- (410.0492,809.1016) -- (338.6085,715.5068) -- (485.4526,774.6960) -- (552.3903,677.8294) -- (541.4753,835.7770) -- cycle; \begin{scope}[fill=c00ffff] \path[fill=cafafde,even odd rule] (288.7831,286.4825) -- (543.3678,317.9365) -- (598.1102,311.7887) -- (364.3741,287.8384) -- cycle; \path[fill=c353564,even odd rule] (288.7831,131.2783) -- (288.7831,286.4825) -- (364.3741,287.8384) -- (364.3741,158.0819) -- cycle; \path[fill=ce9e9ff,even odd rule] (364.3741,158.0820) -- (598.1102,101.9372) -- (598.1102,311.7887) -- (364.3741,287.8384) -- cycle; \path[fill=c4d4d9f,even odd rule] (288.7831,131.2783) -- (543.3678,32.3572) -- (598.1102,101.9372) -- (364.3741,158.0820) -- cycle; \path[fill=cd7d7ff,even odd rule] (543.3678,32.3572) -- (543.3678,317.9365) -- (598.1102,311.7887) -- (598.1102,101.9372) -- cycle; \path[fill=c8686bf,even odd rule] (288.7831,131.2783) -- (543.3678,32.3572) -- (543.3678,317.9365) -- (288.7831,286.4825) -- cycle; \end{scope} \end{tikzpicture} Ресурси глобальної мережі

http://mirror.ctan.org/graphics/pgf/base/doc/generic/pgf/pgfmanual.pdf — Till Tantau. The TikZ and PGF Packages Manual for version 2.10 (англійською).
http://math.et.info.free.fr/TikZ/bdd/TikZ-Impatient.pdf — Gerard Tisseau, Jacques Duma. TikZ pour l’impatient (французькою).
http://www.texample.net/tikz/examples/all/ — приклади застосування TikZ.
http://www.texample.net/tikz/examples/beamer-arrows/ — приклад pdf-презентації з використанням TikZ.
http://elishapeterson.wikidot.com/tikz:diagrams — приклади застосування TikZ на сайті Е.Петерсон (Elisha Peterson).
http://inkscape.org/ — джерело Inkscape.
http://code.google.com/p/inkscape2tikz/ — опис розширення Inkscape до можливості експорту результатів у код TikZ.
http://www.fauskes.net/nb/introduction-to-sketch/ — вступ до Sketch 3D (англійською).
http://www.cord.edu/faculty/ahendric/tex/TikZcheatsheet.pdf — cтислий перелік деяких службових слів.